写在前面

大二上的时候，我就在构思怎么样去写一个类似 Pytorch 的软件。当时大概把三大学习都学的差不多了，就想着自己去实现一些 AI 的组件，渐渐的便想着去了解一下 Pytorch 的代码及其背后的运行原理，只可惜因为时间安排和自身能力的原因而不能立刻着手去学习。

期末后剑圣跟我说到华为那边编写深度学习框架底层算子的事情，寒假时间多了，那确实可以把这件事情捡起来。摸索后我发现国外有两个 Lab 可以来帮助学习深度学习框架，一个是 CMU 的公开课程，一个是 Minitorch。

CMU 的公开课程是 CMU 在 2022 年 9 月开设的一门课程，讲师是 J.Zico Kolter 和陈天奇。这是一门注重实践的课程，课后作业主要是逐步实现一个类似于PyTorch的深度学习框架(类似 Pytorch 和 TensorFlow)。
Minitorch是一个 Torch API 的纯 Python 重新实现，展示了从零开始构建一个张量和自动微分库。最终得到的库能够运行类 Torch 代码。项目创建者为康奈尔大学副教授(pre-tenure)Alexander Rush，这是一门硕士课程。

其中互联网上的评价为 CMU 的公开课程框架性好，易上手；Minitorch 更全面，同时也更难。抉择之下，最后选择了 Minitorch 为我准备学习的课程。我一共花了四天来完成这个 Lab，平均每天用时 6h，收获颇多，便写此博客来记录学习 Minitorch 时的过程。

minitorch

Minitorch

Minitorch 大概有五个部分，项目的创建者将这五个部分分为了五个 Module，依次为计算基础、自动微分、张量、算子加速、AI 组件。

Set Up

该部分主要为 Minitorch 的环境配置

Python venv

我使用的开发环境为 Windows11，并特意为 Minitorch 分配了一个独立的 Python 虚拟环境，使用官方推荐的 Python 3.8，用 venv 命令来创建一个 Python 虚拟环境

1	\the\path\to\python3.8\python.exe -m venv minitorch

这样子便创建好了一个名为 minitorch 的虚拟环境，启动环境后在这里使用 Python 和 Pip 便可以在这个虚拟环境中运行，而不会破坏本机原生的 Python 环境

其实也可以使用 Conda 或 Mamba 来管理 Python 虚拟环境，但说实话我不是很习惯(

Pytest

Minitroch 使用 Pytest 来做代码的正确性检测，说实话这是我第一次使用 Pytest，这东西确实非常好用：它可以模块化管理你的 Test 程序，还可以并行地测试，还可以指定测试时输入的随机数据，更重要的是上手很快，功能繁多但使用并不麻烦。

pytest
pytest -m task0_1
pytest -m task0_1 test\test_autodiff.py
pytest -m task0_1 test\test_autodiff.py::test_one_arg
pytest -m task0_1 test\test_autodiff.py::test_one_arg[fn0]

以上五条指令都是有效的，但测试的范围不一样，体现了 Pytest 的模块性。

Fundamentals

接下来是 Minitorch 的第一个部分，计算基础部分

Operators

这个 Task 主要目的是实现基本的数学计算函数。因为我们后面实现的 Tensor 都需要重载对应的数学运算函数，所以哪怕是最简单的函数都需要我们手动实现一边，做一层封装。

这些函数包括但不限于 Add、Mul、Neg、Exp、Log、Sigmoid、Relu…实现不难比较繁琐。

这里实现的函数都有个特点，那就是只对单个元素或两个元素做计算，而无法对多个元素(比如列表里的所有元素)做计算。

Functional Python

接下来我们将刚刚实现的函数再做一层封装，来实现针对批量元素的处理函数，首先我们可以将批量处理函数概括为三大类：Map、Zip、Reduce。

Map：对单个列表的所有元素做同一操作，比如 Neg。
Zip：对两个列表一一对应的元素做二元操作，比如 Add、Mul。
Reduce：对单个列表的所有元素做递归操作，比如 Sum、Mean。

这部分的函数实现也比较简单，循环操作即可。

Modules

接下来是参数管理，在做深度学习的时候，我们需要对大量的参数做管理：Module 里面会有参数、Module 里面还可能有 Module 的嵌套。我们可以把 Module 抽象为一棵树，接下来我们需要实现几个跟 Module 有关的函数，比如参数和模块的信息获取。

这部分的代码的实现其实就很像是数据结构里对树的操作，核心的思路是使用递归，注意终止条件即可。

Visualization

然后 Minitorch 的第一部分就此完结了，项目的编写者还贴心地为我们写好了可视化的工具，我们可以在这里观察我们刚刚得到的成果。

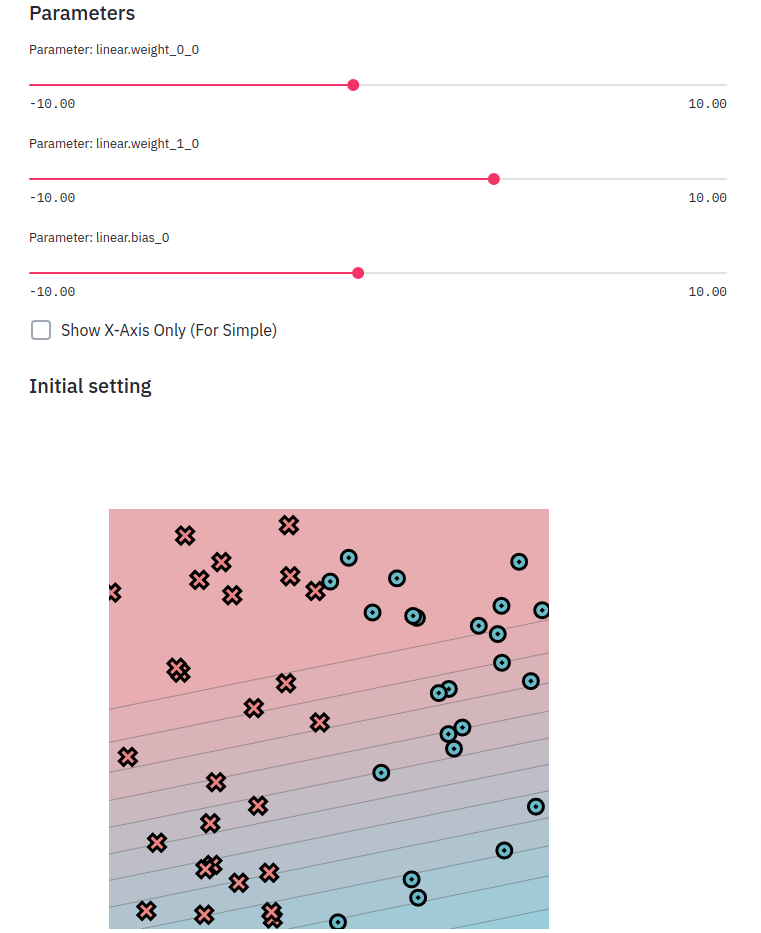
module1-1

Autodiff

从这里开始便能感觉到明显的难度上升，这部分要求我们实现自动微分

Numerical Derivatives

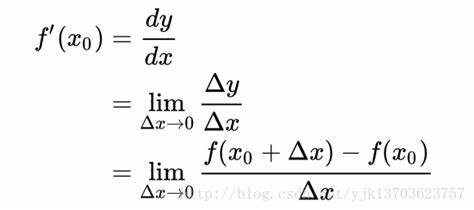
module2-1

在实现自动微分之前，我们需要先了解编程领域中已有的两种计算微分方法，分别是 数值微分 和 公式微分。

数值微分：给函数的参数加上一个很小的偏移量，使用微分的定义直接计算对应的微分值，计算速度快但不准确。
公式微分：依据数学里的求导法则，使用求导公式函数计算对应的微分值，计算精确但可扩展性低。

在这个部分需要依据微分的定义写好一个计算数值微分的函数，这个函数将用于检验我们编写的自动微分准确性。

Scalars

接下来我们开始编写自动微分的代码，首先我们需要对 Module1 写的数学计算的函数做一次封装，使得这些计算不仅能够给出计算的结果(后文用 forward 代替)，还能给出对应的微分值(后文用 backward 代替)。

Chain Rule

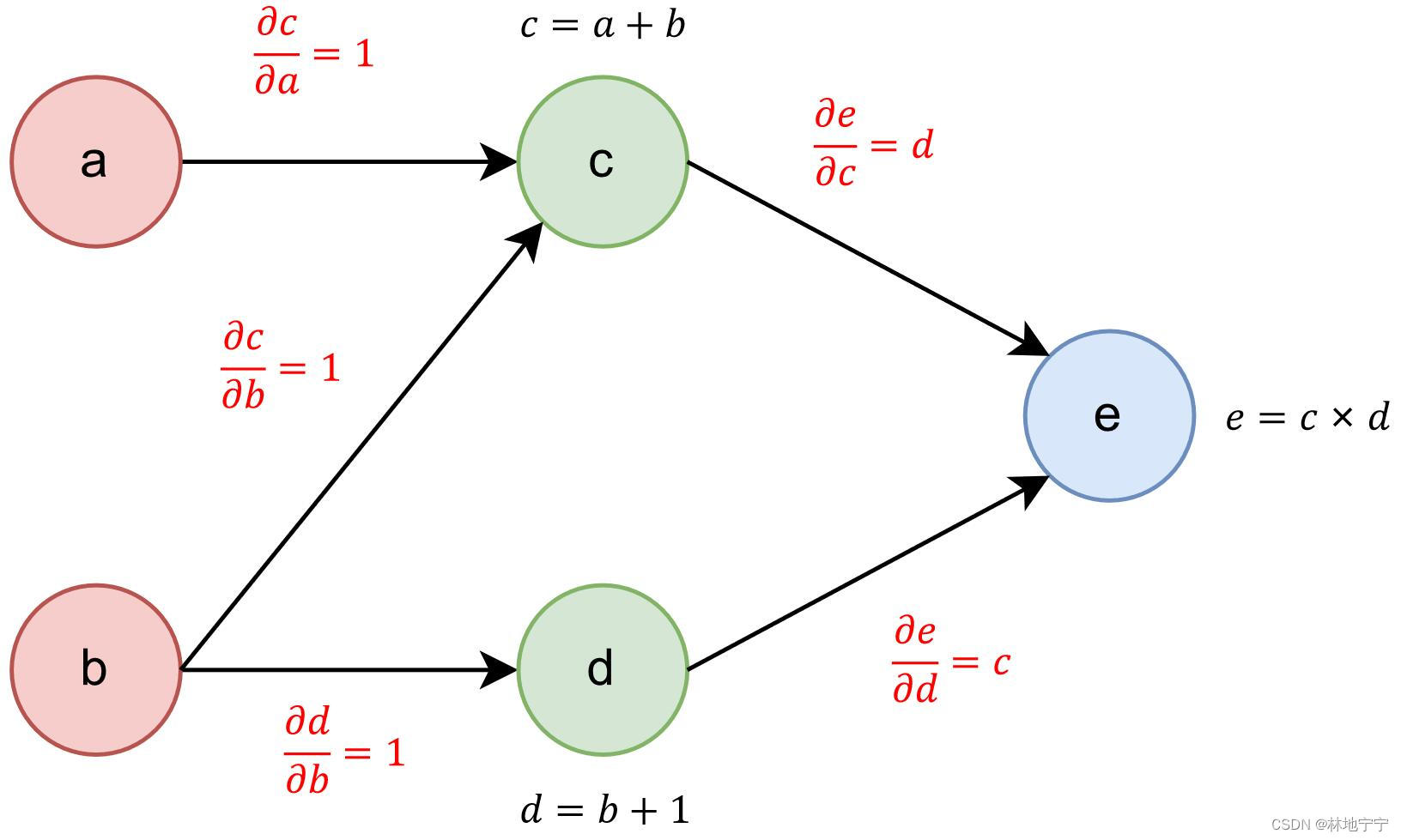
当我们写好了基础函数的 forward 和 backward 的计算逻辑后，我们便可以用基础函数来实现复杂函数的微分计算。

forward 的时候，将每次运算的运算类型、参与运算的对象保存下来；backward 的时候，根据本次运算所使用的运算类型和运行对象来计算本次运算对应的微分值。

因为运算与运算之间是紧密联系的，前一个运算的结果会成为下一个运算的输入，forward 的时候我们会在本地保存一份计算图。

backward 的时候便在这个计算图上反向传递梯度，传递的算法其实就是图遍历的算法，因为计算图可以抽象为一个有向无环图，所以遍历算法推荐使用逆拓扑排序。

module2-2

Backpropagation

这部分需要我们为 Module 编写 backward 函数，其实就是把刚刚写好的 Chain Rule 扩展到 Module 类里的参数上

Training

到目前为止，便写好了 Minitorch 的 Module2 部分，现在可以实现一个简单的网络，只不过里面的输入和矩阵乘法都只能采用非常暴力的实现。对每个参数都单独追踪梯度，计算量直接爆炸，后续会实现 Tensor 类来加速这个过程。

Tensors

在之前的实验中，我们实现了自动微分，forward 时对每一个参数做运算的追踪，backward 对每一个参数做梯队的传播。这样实际上计算量会随着网络参数的增大而指数级提升。在这里我们可以用矩阵的批量运算来代替单个参数的运算，这不仅可以帮我们简化 forward 逻辑的便写，还可以大量减少 backward 时的计算量。

Tensor Data - Indexing

在一些现有的矩阵计算库中(比如 Numpy)，矩阵的底层存储方式其实为一维向量，同时维护一对变量 Shape 和 Stride 来说明该矩阵的形状信息。这么做有这么几个好处：

利用了局部性，一维向量的空间局部性是极佳的，可以提高运行效率。
便于修改矩阵的空间信息，使用一维向量存储数据时可以避免数据的拷贝和迁移。

这部分的实验需要我们去补全这么一个矩阵类，实现一维向量的下标和多维下标的转换。

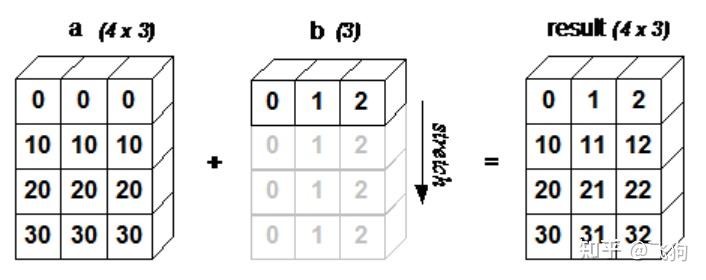
Tensor Broadcasting

在一些现有的矩阵计算库中(比如 Numpy)，矩阵的运算存在广播机制，这可以很方便的实现一些简单的运算。

这部分的代码主要是实现一些后续会用到的广播函数，比如广播后形状的计算、广播坐标的映射，实现起来并不复杂。

module3-1

Tensor Operations

之前的实验实现了一些基础运算(比如 Add、Mul、ReLu)的 forward 和 backward，这里需要将这些函数扩展到 Tensor 上。

在这个部分还需要对 Module1 写好的 Map、Zip、Reduce 函数做一次在 Tensor 上的迁移，比较难缠的是广播机制，广播机制的实现我前前后后大概花了三四个小时，最后的解决方案是在广播之前先计算出广播后的形状大小，再对结果张量的每一个位置做判断，用广播的坐标映射获取到对应输入张量的下标。因为每一个位置之间的运算是独立的，所以可并行性很不错。

值得一提的是 permute 函数的实现，一开始我以为 permute 其实就是形状的修改，而不涉及数据位置的修改，于是写的很简单。直到后面写 Module3/4 时，我才发现我之前写的 permute 函数是错误的。又不得不再折返回来修改。permute 函数的实现也蛮简单，先准备一个全空的结果张量，对结果张量的所有位置做一次遍历，同时计算出结果下标与输入张量下标之间的映射关系，再做数据拷贝即可。

Gradients and Autograd

接下来是对 Tensor 基础函数的 backward 进行实现，backward 的实现跟 Module1 其实非常相像。forward 时保存运算的函数和参与运算的对象，再根据对应的微分法则计算梯度即可。

Training

到目前为止，便写好了 Minitorch 的 Module3 部分，现在可以用 Tensor 实现一个简单的网络，同时里面的输入和矩阵乘法都采用 Tensor 的形式来实现。但是 Tensor 的矩阵乘法还没有实现，目前的矩阵乘法采用多步的基础运算组合实现，一方面并行性较差另一方面会额外创建一个中间张量(多了一笔开销)。

接下来会对矩阵乘法做并行优化，在 CPU 和 GPU 上都可以做优化。

Efficiency

接下来对矩阵乘法做并行优化，在 CPU 和 GPU 上都可以做优化。

Parallelization

Numba 是一款可以将 Python 函数编译为机器代码的编译器，经过 Numba 编译的 Python 代码(仅限数组运算)，其运行速度可以接近 C 或 FORTRAN 语言。
Numba 的编译是 JIT 的，即 Just-In-Time，运行时编译。初次运行时可能需要一段准备的时间，再到后面运行时速度可以接近 C 或 FORTRAN 语言。

Numba 还内置了并行性优化的函数，于是可以用 Numba 自带的 prange 来代替 Python 原生的 range 进行迭代，这可以写出并行性的 Python 计算代码。

这部分的实验要求写出并行性优化后的 Map、Zip、Reduce 的代码，我写这部分的代码前前后后用了差不多三个小时的时间。大体的时间跟之前的实现是非常类似的，主要是对 Numba 的加速原理不太清楚，Numba 只能对 Python 原生运算和部分库的函数做加速，搞懂这个原因后我修改了一些代码逻辑，将复杂的函数放到并行体之外，终于解决了看不懂的报错。

Matrix Multiplication

矩阵乘法的优化便顺畅很多了，有了刚刚的 Debug 经验，很快便结束了这部分的内容。

至此我们实现了并行优化后的矩阵乘法函数。

CUDA Operations

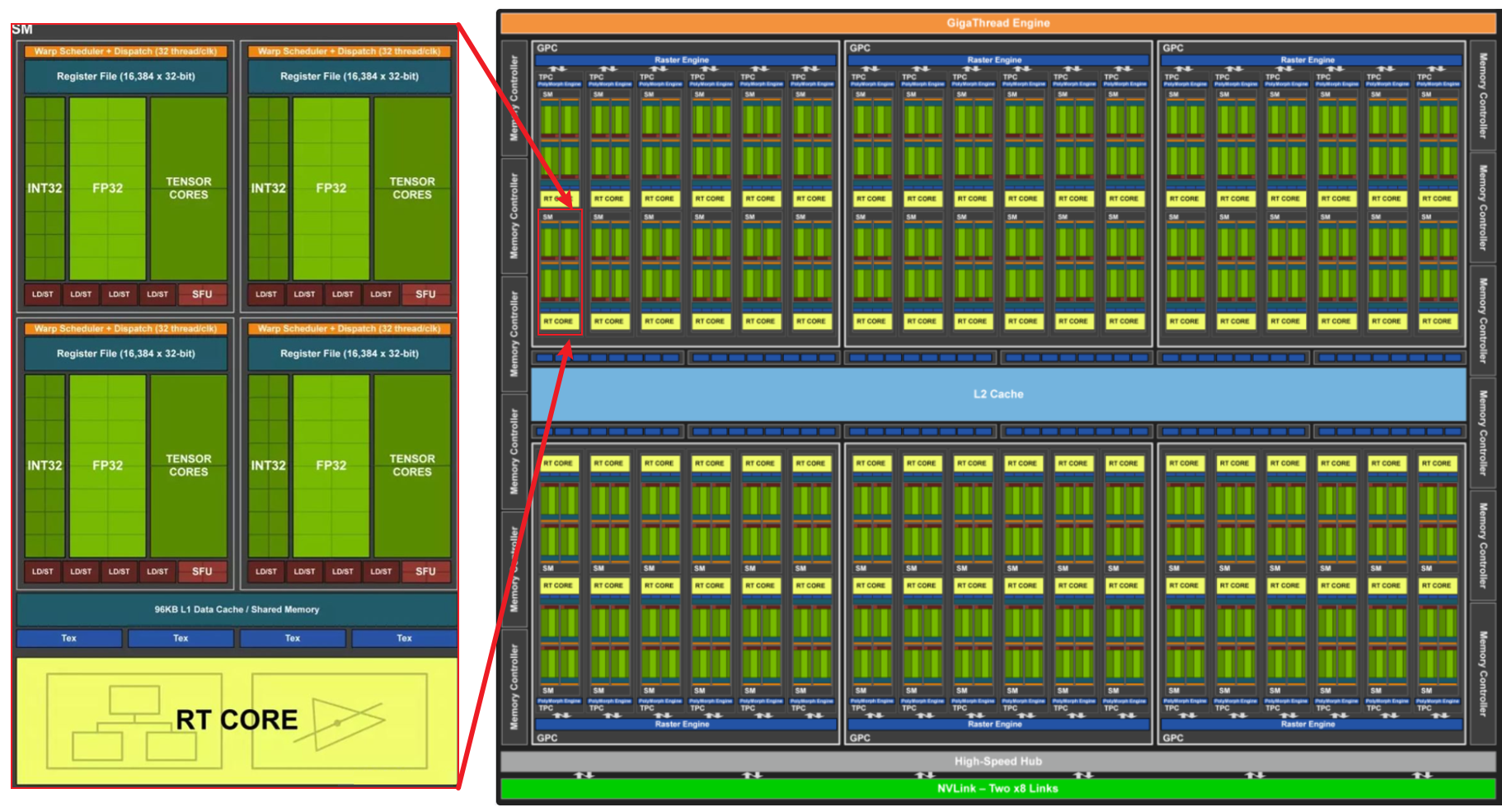
module4-1

(Compute Unified Device Architecture)，又称 CUDA，是由 NVIDIA 推出的通用并行计算架构。解决的是用更加廉价的设备资源，实现更高效的并行计算。和中央处理器相对，GPU 是显卡的核心芯片。而 CUDA 正是暴露了英伟达开发的 GPU 的编程接口。GPU 编程可以使用更多的流处理器、更多的线程数，因此可以更快地为我们加速张量运算。

这部分的实验要求写出用 CUDA 并行性优化后的 Map、Zip、Reduce 的代码，Numba 内置了 CUDA 编程的 Python 接口，我们可以用 Python 代码来写运行在 CUDA 上的程序。这真的是一件非常方便的事情(当然也可以去写 CUDA-C 程序，按照 Python 编译为 .lib 文件后用 Python 做封装调用也行)。

因为我本人之前写过 CUDA-C 的代码，所以这部分的内容对我而言很快就结束了。

CUDA Matrix Multiplication

这部分需要编写使用 CUDA 优化的矩阵乘法函数，跟之前一样，结合已有的代码这部分的内容我也是很快就结束了。

Training

到目前为止，便写好了 Minitorch 的 Module4 部分，对矩阵乘法在 CPU 和 GPU 上都做了并行优化，这大大加速了计算速度。最后一个 module 需要实现深度学习系统的上层组件内容，比如卷积、池化、嵌入层……等到一切成型后，便可以实现卷积神经网络或循环神经网络的功能了。

Networks

这个部分需要去实现深度学习框架的上层组件，比如卷积、池化、嵌入层等。

1D Convolution

首先实现的是一维卷积核，这里有两种方法：

将输入矩阵进行扩充，临时改变输入矩阵和权重矩阵的张量形状，将一维卷积转变为矩阵乘法来进行原运算。这种方法实现便捷，但是中间过程需要对输入矩阵扩充，增大了计算开销。
针对一维卷积额外写 Numba 并行加速后的底层算子，以达到最优效果。

这个部分我的选择是后者。

2D Convolution

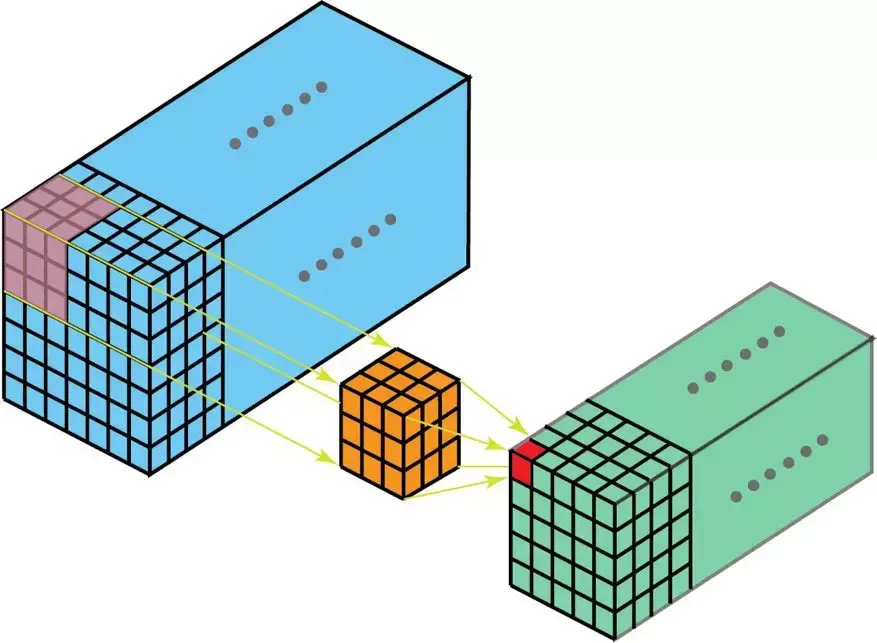
module4-2

其次实现的是一维卷积核，这里依旧有两种方法，我仍然对二维卷积额外写了 Numba 并行加速后的底层算子。

Pooling

池化的实现夜游两种方式：对输入矩阵用 permute 和 Mean/Max 函数来做变换，将池化转变为求矩阵某一维度平均值/最大值的问题。

这里我就采用 permute 和 Mean/Max 的方法了，虽然说这么做 forward 时会产生张量本体数据的移动和拷贝，也许以后可以实现 Pooling 的底层算子实现。

Softmax and Dropout

这两个部分的实现只要熟悉 Softmax 和 Dropout 的原理后就很好办了。值得一提的是 Dropout 的实现，forward 的时候我们需要依据选取的概率来构建 mask，backward 时 mask 遮盖部分梯度直接传 0.0。

Training an Image Classifier

至此我们实现了深度学习框架的上层组件，minitorch 项目贴心地为我们准备了一份 MNIST 手写数字识别，按照正常 Pytorch 的流程实现后，可以正常训练，并且正确率能达到 98% 左右。

结语

这五天的时间过的是很快的，转眼我从不知道如何实现深度学习系统的小白转变为了完整实现国外硕士实验Lab的“小白”，有时 Debug 到脑袋成浆糊，躺在床上很累但又睡不着，不过好在 Minitorch 最终是写完了，这段时间也可以休息一阵子。

再言，互联网上实在是太缺少深度学习框架的相关资料了！特别是中文的教材，简直是技术荒漠！！！

下一次更新博客，估计就是 20 岁生日的时候了。

祝学业进步。